426. Convert-Binary-Search-Tree-to-Sorted-Doubly-Linked-List

difficulty: Medium

section pre{ background-color: #eee; border: 1px solid #ddd; padding:10px; border-radius: 5px; }

Convert a Binary Search Tree to a sorted Circular Doubly-Linked List in place.

You can think of the left and right pointers as synonymous to the predecessor and successor pointers in a doubly-linked list. For a circular doubly linked list, the predecessor of the first element is the last element, and the successor of the last element is the first element.

We want to do the transformation in place. After the transformation, the left pointer of the tree node should point to its predecessor, and the right pointer should point to its successor. You should return the pointer to the smallest element of the linked list.

Example 1:

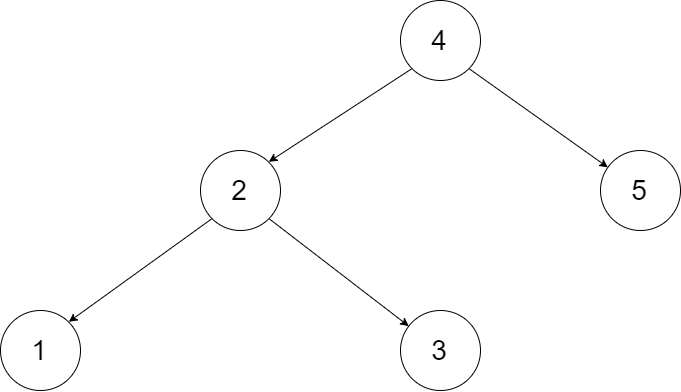
Input: root = [4,2,5,1,3]

Output: [1,2,3,4,5]
Explanation: The figure below shows the transformed BST. The solid line indicates the successor relationship, while the dashed line means the predecessor relationship.

Example 2:

Input: root = [2,1,3]
Output: [1,2,3]

Example 3:

Input: root = []
Output: []
Explanation: Input is an empty tree. Output is also an empty Linked List.

Example 4:

Input: root = [1]
Output: [1]

Constraints:

• -1000 <= Node.val <= 1000

• Node.left.val < Node.val < Node.right.val

• All values of Node.val are unique.

• 0 <= Number of Nodes <= 2000

Method One

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
​
    public Node() {}
​
    public Node(int _val) {
        val = _val;
    }
​
    public Node(int _val,Node _left,Node _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
    private Node head = null;
    private Node last = null;
    
    public Node treeToDoublyList(Node root) {
        if(root == null){
            return null;
        }
        helper(root);
        last.right = head;
        head.left = last;
        return head;
    }
    
    public void helper(Node node){
        if(node == null){
            return;
        }
        
        helper(node.left);
        if(last != null){
            last.right = node;
            node.left = last;
        }else{
            head = node;
        }
        last = node;
        helper(node.right);
    }
}
​

Method 2

class Solution {
    public Node treeToDoublyList(Node root) {
        if(root == null){
            return root;
        }
        Node head = null;
        Node prev = null;
        Node cur = root;
        ArrayDeque<Node> stack = new ArrayDeque<Node>();
        while(!stack.isEmpty() || cur != null ){
            while(cur != null){
                stack.push(cur);
                cur = cur.left;
            }
            cur = stack.pop();

            if(prev == null){
                head = cur;
            }else{
                prev.right = cur;
                cur.left = prev;
            }
            prev = cur;
            cur = cur.right;
        }
        head.left = prev;
        prev.right = head;
        return head;
    }
}

Method 3

真正的 O(1) 还包括 morris traversal.